| Re: 画像の円弧変形 ( No.1 ) |
- 名前:管理人 日時:2018/09/12 00:55
すみません、似ているようで別の話題でしたので、専用にスレッドを立てました
円弧変形は実装可能ですが、微妙に需要があるのか不明でしたので、とりあえず既存の
2Dポリゴンを描画する関数で円弧変形を行う関数を組んでみましたので、よろしければ
こちらのプログラムの関数 DrawWarpGraph を使ってみてください m(_ _)m
プログラムの内容としては「MakeScreen で作成した仮画面に『上下左右に跳ね回る四角形』を
大量に描画して、その仮画面を DrawWarpGraph で扇形に変形して画面に描画する」
といったものとなっています
#include "DxLib.h"
#include <math.h>
// 変形描画用の頂点の横方向の数
#define WVERTNUM 64
// 変形描画用の頂点の縦方向の数
#define HVERTNUM 16
// 変形描画用の頂点の配列
VERTEX2D Vertex[ WVERTNUM ][ HVERTNUM ] ;
// 変形描画用の頂点インデックスの配列
unsigned short Index[ ( WVERTNUM - 1 ) * ( HVERTNUM - 1 ) * 6 ] ;
// 扇形変形描画を行う関数
void DrawWarpGraph(
float CenterX, float CenterY, // 扇の円の中心座標
float Angle, // 扇を描く角度の範囲( 単位:ラジアン )
float NearR, float FarR, // 扇を描く円の内側の半径と外側の半径
int GrHandle ) // 扇状に描くグラフィックハンドル
{
float VSize ;
int GraphW, GraphH ;
int TextureW, TextureH ;
unsigned short *ind ;
int i, j ;
float r ;
float ang ;
float Cos, Sin ;
COLOR_U8 white = GetColorU8( 255,255,255,255 ) ;
// 扇の縦幅を算出
VSize = FarR - NearR ;
// 内側の半径の値の方が外側の半径の値より大きかったらエラー
if( VSize <= 0.0f )
{
return ;
}
// グラフィックハンドルの画像のサイズを取得
GetGraphSize( GrHandle, &GraphW, &GraphH ) ;
// グラフィックハンドルのテクスチャのサイズを取得
GetGraphTextureSize( GrHandle, &TextureW, &TextureH ) ;
// 扇状に描くための頂点の準備
for( i = 0 ; i < WVERTNUM ; i ++ )
{
// 頂点を配置する角度を計算
ang = -DX_PI_F / 2 - Angle / 2.0f + Angle / ( WVERTNUM - 1 ) * i ;
Cos = cos( ang ) ;
Sin = sin( ang ) ;
for( j = 0 ; j < HVERTNUM ; j ++ )
{
// 半径の計算
r = FarR - VSize / ( HVERTNUM - 1 ) * j ;
// 座標の計算、扇状に頂点が並ぶようにする
Vertex[ i ][ j ].pos.x = Cos * r + CenterX ;
Vertex[ i ][ j ].pos.y = Sin * r + CenterY ;
// 固定値
Vertex[ i ][ j ].pos.z = 0.0f ;
Vertex[ i ][ j ].rhw = 1.0f ;
// 頂点カラーは真っ白
Vertex[ i ][ j ].dif = white ;
// UV値の計算
Vertex[ i ][ j ].u = ( float )GraphW / ( WVERTNUM - 1 ) * i / ( float )TextureW ;
Vertex[ i ][ j ].v = ( float )GraphH / ( HVERTNUM - 1 ) * j / ( float )TextureH ;
}
}
// 頂点インデックスの準備
ind = Index ;
for( i = 0 ; i < WVERTNUM - 1 ; i ++ )
{
for( j = 0 ; j < HVERTNUM - 1 ; j ++ )
{
// 各ポリゴンの頂点番号をセット
ind[ 0 ] = j + i * HVERTNUM ;
ind[ 1 ] = j + ( i + 1 ) * HVERTNUM ;
ind[ 2 ] = j + 1 + i * HVERTNUM ;
ind[ 3 ] = j + 1 + ( i + 1 ) * HVERTNUM ;
ind[ 4 ] = ind[ 2 ] ;
ind[ 5 ] = ind[ 1 ] ;
ind += 6 ;
}
}
// 扇状に描くためのポリゴン群を描画
DrawPolygonIndexed2D(
&Vertex[ 0 ][ 0 ],
WVERTNUM * HVERTNUM,
Index,
( WVERTNUM - 1 ) * ( HVERTNUM - 1 ) * 2,
GrHandle,
FALSE
) ;
}
// 画面を飛び回るオブジェクトの数
#define OBJNUM 1000
// 画面を飛び回るオブジェクトの情報
struct Obj
{
int x, y ;
int xadd, yadd ;
int size ;
int color ;
} ;
// 画面を飛び回るオブジェクトの情報の配列
Obj obj[ OBJNUM ] ;
int WINAPI WinMain( HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow )
{
int ScreenHandle ;
int i ;
// ウインドウモードで起動
ChangeWindowMode( TRUE );
// DXライブラリの初期化
if( DxLib_Init() < 0 ) return -1 ;
// 仮画面を作成
ScreenHandle = MakeScreen( 640, 480, TRUE ) ;
// 画面を飛び回るオブジェクトの情報を準備
for( i = 0 ; i < OBJNUM ; i ++ )
{
obj[ i ].x = GetRand( 640 ) ;
obj[ i ].y = GetRand( 480 ) ;
obj[ i ].xadd = GetRand( 3 ) + 1 ;
if( GetRand( 100 ) < 50 ) obj[ i ].xadd = -obj[ i ].xadd ;
obj[ i ].yadd = GetRand( 3 ) + 1 ;
if( GetRand( 100 ) < 50 ) obj[ i ].yadd = -obj[ i ].yadd ;
obj[ i ].size = GetRand( 8 ) + 8 ;
obj[ i ].color = GetColor( GetRand( 255 ), GetRand( 255 ), GetRand( 255 ) ) ;
}
// メインループ
while( ProcessMessage() == 0 )
{
// 描画先を仮画面に設定
SetDrawScreen( ScreenHandle ) ;
// 画面クリア
ClearDrawScreen() ;
// オブジェクトを動かす+描画
for( i = 0 ; i < OBJNUM ; i ++ )
{
obj[ i ].x += obj[ i ].xadd ;
if( obj[ i ].x < 0 || obj[ i ].x > 640 )
obj[ i ].xadd = -obj[ i ].xadd ;
obj[ i ].y += obj[ i ].yadd ;
if( obj[ i ].y < 0 || obj[ i ].y > 480 )
obj[ i ].yadd = -obj[ i ].yadd ;
DrawBox(
obj[ i ].x - obj[ i ].size, obj[ i ].y - obj[ i ].size,
obj[ i ].x + obj[ i ].size, obj[ i ].y + obj[ i ].size,
obj[ i ].color, TRUE ) ;
}
// 描画先を裏画面にする
SetDrawScreen( DX_SCREEN_BACK ) ;
// 仮画面に描画した内容を扇状に描画
DrawWarpGraph( 320.0f, 680.0f, DX_PI_F / 2.0f, 270.0f, 600.0f, ScreenHandle ) ;
// 裏画面の内容を表画面に反映する
ScreenFlip() ;
}
// DXライブラリの後始末
DxLib_End();
// ソフトの終了
return 0;
}
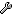 |
| Re: 画像の円弧変形 ( No.2 ) |
- 名前:たろう(解決) 日時:2017/05/24 03:08
ありがとうございます!! たろうです。
早速試しました。完全にフォトショップの円弧変形と同じ変形を再現できました。
というより使い勝手はむしろ上かもしれません。ありがたく使わせていただきます!!
完璧なので、私としては専用のものを実装していただかなくても大丈夫です。
すでにあるもので再現できるとは思いもよらず
何度目でしょうか、またお手数をおかけしてしまいました。いつもすみませんm(_ _)m
ありがとうございました!!
|
| Re: 画像の円弧変形 ( No.3 ) |
- 名前:8127 日時:2018/09/11 23:35
管理人様、
自由変形を試してみたかったのでこのソースを拝借させていただきましたが、
実行するたびに結果が異なる変な挙動になりました。(ScreenHandleの作成に成功したり失敗したりする)
ソース中、
// 仮画面を作成
ScreenHandle = MakeScreen( 640, 480, 32 ) ;
とありますが、MakeScreenの第三引数は32ではなくてTRUEが正しいと思います。
TRUEに変更したところ期待通り動作しました。
|
| Re: 画像の円弧変形 ( No.4 ) |
- 名前:管理人 日時:2018/09/12 00:57
ご指摘ありがとうございます
MakeScreen( 640, 480, TRUE ) ;
に修正しました
|
| Re: 画像の円弧変形 ( No.5 ) |
- 名前:たろう 日時:2018/12/16 03:25
いつもすみません、たろうです。
以前作っていただいた、DrawWarpGraphを使用させていただいているのですが
これに扇の内側に行くほど小さくなるような表現を追加したいと思い、
その「内側に行くほど小さくなる」程度を
下に貼らせていただいたプログラムのDrawWarpGraph()内の
「////ここです1」の部分に、関数「扇Lnc4」を挟んで
コントロール出来るようにしたのですが、
加えて、扇状になった画像の任意の位置をマウスで示した時、
その位置が元画像のどの位置に当たるのかを返す関数「逆扇変換」を作り、
ここまではうまくいったのですが、
「逆扇変換」で取得した位置をまた扇画像の位置に戻す関数
「扇変換」をうまく作ることが出来ず困っています(-_-;)
下のプログラムを起動していただくと、
左に元画像、右にその画像を扇形に変形したものが表示されるのですが
扇画像のマス目をマウスで示すと、その座標が「逆扇変換」で変換され(※////ここです2)
元画像の同じマス目を赤点で正確に示すと思います。
ですがその座標がさらに「扇変換」で扇画像に戻されて表示される赤点と(※////ここです3)
元画像の赤点はどうしてもずれてしまいます。
DrawWarpGraphに「扇Lnc4」を差し込んだのと同じ原理で
簡単に出来ると思ったのですが
DrawPolygonIndexed2DやVERTEX2D
が理解できていないので、
同じような座標変化を「扇変換」で再現できず
困っています。よろしければアドバイスを頂けますでしょうか?
DrawWarpGraphは私でも理解しやすいよう変数名を変えてありますが
「////ここです1」の部分以外は頂いた物と同じです
またWinMainに長々書いてある部分は「////ここです2」「////ここです3」以外の所は
テンキーの+-で扇の角度を変更できるようにして、チェックをしやすくするためのもので
あまり関係のない部分です。
大変ずうずうしい質問になってしまいましたが、
よろしければ、なにとぞお知恵をおかしいただけると助かりますm(_ _)m
////////////////////////////////////////////////////////////////////////////////////////////
#include "DxLib.h"
#include <math.h>
#define dbl double
#define flt float
#define PI DX_PI_F
#define PI倍 DX_TWO_PI_F
#define PI半 (DX_PI_F/2.0F)
const int 割数W = 64 , 割数H = 16 ;
VERTEX2D Vertex[ 割数W ][ 割数H ] ;
unsigned short Index[ (割数W-1) * (割数H-1) * 6 ] ;
int 画W=801, 画H=401 ;
int OUG_X=832;
int OUG_Y=400;
int OUG_Xh=OUG_X/2;
int OUG_Yh=OUG_Y/2;
flt 度W= PI半;//扇表示幅ラジアン
flt 度A=-PI半;//扇の傾き
flt 円心x=1270;//扇を作る円の中心
flt 円心y=1000;//扇を作る円の中心
flt 外Y=600;//円心yから扇の外側までの距離(半径)
flt 内Y=200;//円心yから扇の内側までの距離(半径)
flt 幅Y= 外Y - 内Y ;
inline flt 扇Lnc4(flt i, flt ap=1.0f, flt bp=1.0f)
{
flt a率=1/ap;
return i*a率*bp;
}
void 扇変換( flt *x,flt *y )
{
*y=*y-( *y * 扇Lnc4(画H-*y, (flt)画H, ((-度W)/PI)) );
flt ang = 度A - (度W / 2.0f) + (度W / (flt)画W) * (*x) ;
flt Cos = cos( ang ) ;
flt Sin = sin( ang ) ;
flt r = 外Y - (幅Y/(flt)画H) * (*y) ;
*x = Cos * r + 円心x ;
*y = Sin * r + 円心y ;
}
void 逆扇変換( flt *x,flt *y )
{
flt RRR=sqrt((*x-円心x)*(*x-円心x)+(*y-円心y)*(*y-円心y));
*x-=円心x;
*y-=円心y;
flt ang;
if(度W>=0){ ang= atan2(*y,*x)+PI-(PI半-度W)-度A-PI半; }
else { ang= atan2(*y,*x)+PI-(PI半-度W)+度A-PI半;RRR*=-1;}
*x = ang *(画W/度W)-画W/2;
*y = ((画H*(外Y/画H))-RRR)*(画H/幅Y);
*y=*y+( *y * 扇Lnc4(画H-*y, (flt)画H, ((-度W)/PI) ));
}
void DrawWarpGraph( int 画 )
{
int TextureW, TextureH ;
unsigned short *ind ;
int i, j ;
flt r, ang , Cos , Sin ;
COLOR_U8 white = GetColorU8( 255,255,255,255 ) ;
if( 幅Y <= 0.0f ){return ;}
GetGraphSize( 画, &画W, &画H ) ;
GetGraphTextureSize( 画, &TextureW, &TextureH ) ;
for( i = 0 ; i < 割数W ; i ++ )
{
ang = 度A - 度W / 2.0f + 度W / ( 割数W - 1 ) * i ;
Cos = cos( ang ) ;
Sin = sin( ang ) ;
for( j = 0 ; j < 割数H ; j ++ )
{
r = 外Y - 幅Y / ( 割数H - 1 ) * j ;
Vertex[ i ][ j ].pos.x = Cos * r + 円心x ;
Vertex[ i ][ j ].pos.y = Sin * r + 円心y ;
Vertex[ i ][ j ].pos.z = 0.0f ;
Vertex[ i ][ j ].rhw = 1.0f ;
Vertex[ i ][ j ].dif = white ;
Vertex[ i ][ j ].u = ( float )画W / ( 割数W - 1 ) * i / ( float )TextureW ;
Vertex[ i ][ j ].v = ( float )画H / ( 割数H - 1 ) * j / ( float )TextureH ;
Vertex[ i ][ j ].v = Vertex[ i ][ j ].v + ( Vertex[ i ][ j ].v * 扇Lnc4( 画H-Vertex[ i ][ j ].v*(flt)画H , (flt)画H, ((-度W)/PI)) );////ここです1
}
}
ind = Index ;
for( i = 0 ; i < 割数W - 1 ; i ++ )
{
for( j = 0 ; j < 割数H - 1 ; j ++ )
{
ind[ 0 ] = j + i * 割数H ;
ind[ 1 ] = j + ( i + 1 ) * 割数H ;
ind[ 2 ] = j + 1 + i * 割数H ;
ind[ 3 ] = j + 1 + ( i + 1 ) * 割数H ;
ind[ 4 ] = ind[ 2 ] ;
ind[ 5 ] = ind[ 1 ] ;
ind += 6 ;
}
}
DrawPolygonIndexed2D( &Vertex[ 0 ][ 0 ], 割数W * 割数H, Index, ( 割数W - 1 ) * ( 割数H - 1 ) * 2, 画, TRUE ) ;
}
/////////////////////////////////////////////////////////////
int WINAPI WinMain( HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow )
{
ChangeWindowMode( TRUE );
SetGraphMode(1700,500,16);
if( DxLib_Init() < 0 ) return -1;
int 赤=GetColor( 245 ,35 ,25 ) ,鼠x , 鼠y ,鼠o;
int 画=MakeScreen(画W,画H,TRUE);
SetDrawScreen( 画 );
for(int x=0;x<=8;x++){DrawLine(100*x,0,100*x,400,GetColor( 200 ,200 ,200 ),TRUE);}
for(int y=0;y<=4;y++){DrawLine(0,100*y,800,100*y,GetColor( 200 ,200 ,200 ),TRUE);}
SetDrawScreen( DX_SCREEN_BACK );
while( ProcessMessage() == 0 )
{
ClearDrawScreen() ;
GetMousePoint( &鼠x , &鼠y ) ;
if(CheckHitKey(KEY_INPUT_ADD) ){度W-=0.1f;}
if(CheckHitKey(KEY_INPUT_SUBTRACT)){度W+=0.1f;}
flt 中Y=(OUG_Xh)/tan(度W/2);
if(度W>0){中Y= sqrt((OUG_Yh)*(OUG_Yh)+(中Y*中Y));}
else {中Y=-sqrt((OUG_Yh)*(OUG_Yh)+(中Y*中Y));}
外Y=中Y+(OUG_Yh);
内Y=中Y-(OUG_Yh);
円心y=外Y+(400-OUG_Y)/2;
幅Y= 外Y - 内Y ;
DrawRotaGraph2F( 0,0, (0),(0), 1,0,画, TRUE, FALSE);
DrawWarpGraph( 画 );
flt x4=鼠x,y4=鼠y;
逆扇変換( &x4, &y4 ); DrawCircle(x4,y4,2,赤,TRUE);////ここです2
扇変換( &x4, &y4 ); DrawCircle(x4,y4,2,赤,TRUE);////ここです3
ScreenFlip();
}
DxLib_End();
return 0;
}
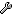 |
| Re: 画像の円弧変形 ( No.6 ) |
- 名前:管理人 日時:2018/12/16 19:28
『逆扇変換』の際の y座標を計算する際に使用した y座標を保持しておくようにしたところ、
座標がずれなくなりました( y2 という引数がそれです )
void 扇変換( flt *x,flt *y, flt y2 )
{
*y=*y-( y2 * 扇Lnc4(画H-y2, (flt)画H, ((-度W)/PI)) );
flt ang = 度A - (度W / 2.0f) + (度W / (flt)画W) * (*x) ;
flt Cos = cos( ang ) ;
flt Sin = sin( ang ) ;
flt r = 外Y - (幅Y/(flt)画H) * (*y) ;
*x = Cos * r + 円心x ;
*y = Sin * r + 円心y ;
}
void 逆扇変換( flt *x,flt *y, flt *y2 )
{
flt RRR=sqrt((*x-円心x)*(*x-円心x)+(*y-円心y)*(*y-円心y));
*x-=円心x;
*y-=円心y;
flt ang;
if(度W>=0){ ang= atan2(*y,*x)+PI-(PI半-度W)-度A-PI半; }
else { ang= atan2(*y,*x)+PI-(PI半-度W)+度A-PI半;RRR*=-1;}
*x = ang *(画W/度W)-画W/2;
*y = ((画H*(外Y/画H))-RRR)*(画H/幅Y);
*y2 = *y;
*y=*y+( *y2 * 扇Lnc4(画H-*y2, (flt)画H, ((-度W)/PI) ));
}
flt x4=鼠x,y4=鼠y, y42;
逆扇変換( &x4, &y4, &y42 ); DrawCircle(x4,y4,2,赤,TRUE);////ここです2
扇変換( &x4, &y4, y42 ); DrawCircle(x4,y4,2,赤,TRUE);////ここです3
この y2 抜きで『扇変換』を正しく行うのは困難です
( 扇Lnc4 周りの計算で『逆扇変換』の際の y の値が必要なため )
y2 抜きで『扇変換』を正しく行えるようにする場合は計算式を変更する必要があると思います…
|
| Re: 画像の円弧変形 ( No.7 ) |
- 名前:たろう 日時:2018/12/16 21:33
たろうです、お忙しいところ、ご返信ありがとうございますm(_ _)m
ゲーム自体は平面の座標(元座標)で管理して
背景を表示するときだけ背景をDrawWarpGraphで扇状に変形させ、
キャラクターは、絵は扇状に変形させず表示座標だけ扇状に合わせて表示する
というようにしたいと思っています。
その際、キャラクターが例えば鉄砲を持っていて、その鉄砲の先
から弾を発射するときに、その鉄砲の先と、発生させる弾
の位置を揃えようとすると、弾は「元座標」に
発生させる必要があるので、「逆扇変換」の時に使った数値を
「扇変換」に使うという方法ですと、発生させた弾は
動いて座標が変わるので、この場合使用できなそうです(-_-;)
そうなりますと、、
>y2 抜きで『扇変換』を正しく行えるようにする場合は計算式を変更する必要がある
ということになりますが、
奥に行くほど小さくなるというような計算を、普通どのように表すのかと言うのが
分からず、また小さくなる割合をできれば見た目が良くなるようにコントロールしたい
というのもありましてあのような計算方法にしたのですが、
例えば奥(Y座標)に行くほど小さくなるという表現を計算する際の
セオリーなどがわかれば、可逆的に計算できると思うのですが
できればヒントをいただけませんでしょうか?
重ね重ねすみませんm(_ _)m
|
| Re: 画像の円弧変形 ( No.8 ) |
- 名前:管理人 日時:2018/12/17 00:33
> 例えば奥(Y座標)に行くほど小さくなるという表現を計算する際の
> セオリーなどがわかれば、可逆的に計算できると思うのですが
> できればヒントをいただけませんでしょうか?
私は擬似3Dのゲームの開発経験が無いのでセオリーはわかりません、すみません
> 奥に行くほど小さくなるというような計算を、普通どのように表すのかと言うのが
> 分からず、また小さくなる割合をできれば見た目が良くなるようにコントロールしたい
> というのもありましてあのような計算方法にしたのですが、
計算の基準となっているのが
> Vertex[ i ][ j ].v = Vertex[ i ][ j ].v + ( Vertex[ i ][ j ].v * 扇Lnc4( 画H-Vertex[ i ][ j ].v*(flt)画H , (flt)画H, ((-度W)/PI)) );////ここです1
こちらの、テクスチャの v 座標を変更することで『扇の内側に行くほど小さくなるような表現』を実現して
いるのが原因のような気がします( そのため、計算の基準が『逆扇変換』となってしまい、『逆扇変換』で
使用するパラメータが無いと『扇変換』ができない状態になっています )
v を操作するのではなく pos.x, pos.y, pos.z を操作することで『扇の内側に行くほど小さくなるような表現』を
するようにすれば、『扇変換』が計算の基準となるため、『逆扇変換』のパラメータが無いと『扇変換』ができない、
という事態にはならないと思います
なので、v を操作するのではなく pos.x, pos.y, pos.z を操作することで『扇の内側に行くほど小さくなるような表現』を
するような処理に変更すれば問題は解決すると思います
|
| Re: 画像の円弧変形 ( No.9 ) |
- 名前:たろう(解決) 日時:2018/12/17 20:54
ご返信いただきありがとうございます。
pos.x, pos.y, pos.zを操作して扇変換を計算の基準にすることは出来ましましたが
そうすると今度は逆扇変換がずれるので、やはり思うような結果は得られませんでした。
どうも根本的に考え方が違うようで、もう少し良く考えて別の方法を試すか
もしくは出来たとしても処理が重くなりそうでもありますし、
見た目も良くなるかは微妙なので
諦めようかと思います。
円弧変形自体は解決のスレなので、解決に戻させていただきます。
お忙しい中お時間をいただきありがとうございましたm(_ _)m
|
|